This is part 2 of “Examples for performance optimization in C and C++”, you can find part 1 here: Examples for performance optimization in C and C++, Part 1
In our last example, we have seen how we can gain performance by avoiding multiple calculations of the same value and by reordering loops. This time we will look at adapting generic library code for our use case. We will also look at another case of loop reordering. The code presented here is again from SPTK.
Adapting library code
As in part 1, we identified another function hogging our CPU, namely “mgc2mgc” as shown below:
void mgc2mgc(double* c1, const int m1, const double a1, const double g1,
double* c2, const int m2, const double a2, const double g2) {
double a;
static double* ca = NULL;
static int size_a;
if (ca == NULL) {
ca = dgetmem(m1 + 1);
size_a = m1;
}
if (m1 > size_a) {
free(ca);
ca = dgetmem(m1 + 1);
size_a = m1;
}
a = (a2 - a1) / (1 - a1 * a2);
if (a == 0) {
movem(c1, ca, sizeof(*c1), m1 + 1);
gnorm(ca, ca, m1, g1);
gc2gc(ca, m1, g1, c2, m2, g2);
ignorm(c2, c2, m2, g2);
}
else {
freqt(c1, m1, c2, m2, a);
gnorm(c2, c2, m2, g1);
gc2gc(c2, m2, g1, c2, m2, g2);
ignorm(c2, c2, m2, g2);
}
return;
}
Especially “gc2gc”:
void gc2gc(double* c1, const int m1, const double g1, double* c2, const int m2,
const double g2) {
int i, min, k, mk;
double ss1, ss2, cc;
static double* ca = NULL;
static int size;
if (ca == NULL) {
ca = dgetmem(m1 + 1);
size = m1;
}
if (m1 > size) {
free(ca);
ca = dgetmem(m1 + 1);
size = m1;
}
movem(c1, ca, sizeof(*c1), m1 + 1);
c2[0] = ca[0];
for (i = 1; i <= m2; i++) {
ss1 = ss2 = 0.0;
min = (m1 < i) ? m1 : i - 1;
for (k = 1; k <= min; k++) {
mk = i - k;
cc = ca[k] * c2[mk];
ss2 += k * cc;
ss1 += mk * cc;
}
if (i <= m1) {
c2[i] = ca[i] + (g2 * ss2 - g1 * ss1) / i;
}
else {
c2[i] = (g2 * ss2 - g1 * ss1) / i;
}
}
return;
}
Running our time measurements on the target device for the piece of code in question emits the following:
[DNN-PROFILER] Feature transformation: 1601ms.
Which is clearly a problem.
The interesting part is this:
if (i <= m1) {
c2[i] = ca[i] + (g2 * ss2 - g1 * ss1) / i;
}
else {
c2[i] = (g2 * ss2 - g1 * ss1) / i;
}
“ca” is a copy of “c1”, so we figure out that the input array “c1” is processed and then output to “c2”, where “m1” and “m2” specify the array lengths. Furthermore we can see that in the first if-branch, “c2[i] = ca[i]” if “g2 == g1 == 0.0”. In the second branch, we get “c2[i] = 0.0” when “g2 == g1 == 0.0”.
Now let’s again take a look at the call to “gc2gc”:
gc2gc(c2, m2, g1, c2, m2, g2);
So in the case of “mgc2mgc”, “gc2gc” is called with the same array (+ length) for input and output, which means the second if-branch in the code above will never be called. Now we are interested in “g1” and “g2”, so we take a step up in the hierarchy to find:
mgc2mgc(mgc, m, a, g, c, flng / 2, 0.0, 0.0);
Woah, seems “g2 == 0.0”.
So let’s take another step up to check “g”:
static const double GAMMA = 0.0; ... mgc2sp(c, m, alpha, gamma, x, y, l);
Duh!
So we conclude that in our use case of the library function, “gc2gc” only copies the input array to a temporary array, does a lot of calculations, and then copies it back to the input array… unmodified!
So let’s add a quick and dirty fix for this:
if (g1 > 0.0 || g2 > 0.0) {
gc2gc(c2, m2, g1, c2, m2, g2);
}
Let’s look at the original time measurement again:
[DNN-PROFILER] Feature transformation: 1601ms.
Now compile and re-run:
[DNN-PROFILER] Feature transformation: 324ms.
Well, I guess that’s significant.
Loop reordering 2
Here I only want to briefly show another case of reordering loops to achieve sequential memory access and pulling out variables.
You can find a longer example in Examples for performance optimization in C and C++, Part 1. So this time we will just look at the git diff of the changes:
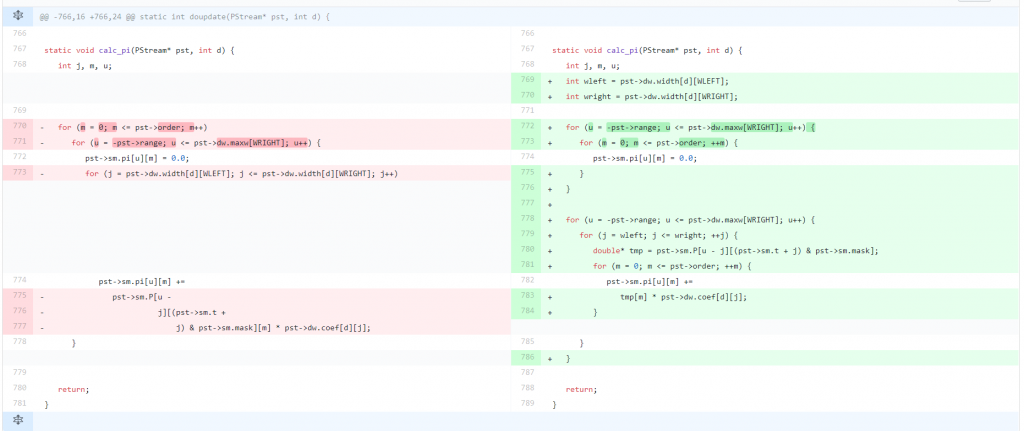
Of essence in this example is the following memory access:
pst->sm.pi[u][m] += pst->sm.P[u - j][(pst->sm.t + j) & pst->sm.mask][m] * pst->dw.coef[d][j];
We can see that with the index calculations we end up jumping around in memory, as “j” is modified in the most inner loop. To solve this, we have to pull out the zero-initialization so we can then reorder the loops so that “pst->sm.P[u – j][(pst->sm.t + j) & pst->sm.mask]” stays the same for the most inner loop and we are iterating over m. Unfortunately we sacrifice the sequential access to “pst->dw.coef[d][j]”, but with “j” iterating over a much smaller value range, we still gain performance in the end.
On our target device, this reordering gained us 50ms for the same test data as in the other examples.
Conclusion
We have seen that using library code as a blackbox might result in unneccessary bloat that directly affects the performance of our application, We have introduced a small fix that significantly decreased CPU consumption for our use case.
The takeaway message is: when dealing with abstractions, take a look at the actual instance you are dealing with in your application. Might well be that it is not well-suited and introduces unneccessary bloat. We have also looked at another case of loop reordering to avoid crazy jumps in memory.
Recent Comments